
Dossiers-parcours
*Du géocentrisme à l’héliocentrisme : les résistances des discours à la rationalité scientifique
Pour se construire le discours scientifique se détache lentement de ses liens avec la poésie, comme le symbolise l’union d’Uranie, la Muse de l’astronomie avec le globe.

– Commentez la symbolique de la sculpture.
***Les Présocratiques
Comment est née la science ? Anaximandre, premier scientifique
Conférence donnée à l’IAP le 1er février 2011, par Carlo Rovelli, Professeur à l’Université de la Méditerranée (Centre de physique théorique de Luminy, Marseille).
Anaximandre, fils de Praxiade, était de Milet. Il admettait pour principe et élément des choses l’infini, (…) que l’infini lui-même, dans son ensemble, est immuable. La terre, selon lui, est située au milieu de l’univers ; elle en est le centre. (…) Il dessina le premier la circonférence de la terre et de la mer.
Diogène Laërce, Vies des philosophes, II, 1-2
[marron]Exercice : Rédiger un dossier sur l’astronomie des Présocratiques, en choisissant l’un d’entre eux en particulier. Montrez comment le langage introduit du trouble dans le discours scientifique. [/marron]
**Les cosmologies et les résistances à la science
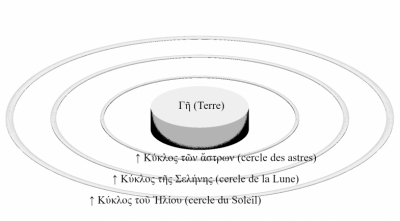
Les premières tentatives d’apporter[violet] une explication rationnelle au monde[/violet] furent le fait de philosophes ioniens du VIIe siècle avant notre ère, comme Thalès de Milet, Anaximandre ou Anaximène. Apparurent alors plusieurs cosmologies afin d’expliquer le monde à l’aide de lois naturelles, plutôt qu’en faisant appel à la magie ou aux caprices des dieux. Le projet scientifique est de trouver une cohérence là où il ne semble pas en avoir. Cependant l’irrationnel ne se loge pas seulement dans ce qui relève classiquement de la superstition. Les savants ont des convictions qui peuvent aussi expliquer leur refus de certains modèles d’explication mathématique.
Les persistances des présupposés platoniciens : le modèle des cercles et l’idée d’harmonie. Les grands dogmes du modèle sphérique : une Terre ronde et immobile au centre, et le mouvement circulaire uniforme des astres. Eudoxe de Cnide a, le premier, conçu un modèle mathématique à 27 sphères traduisant la course de l’ensemble des corps célestes. Leurs travaux nous ont été transmis par des poètes tel Aratos de Soles et des savants plus tardifs (Strabon, Ptolémée, Macrobe).
– Que nous donne à penser ce croisement du discours de la rationalité mathématique et de la poésie ?
***Le système de Ptolémée

« Ce qui a conduit les anciens à l’idée de la sphère, c’est surtout la révolution des étoiles toujours visibles, que l’on voit s’accomplir circulairement autour d’un seul et même centre »
Ptolémée, Syntaxe mathématique, I, 3
Avec les huit livres de sa Géographie, Ptolémée, astronome, astrologue, géographe vivant à Alexandrie au IIe siècle après J.-C., transmit à l’Occident le résultat de plus de sept siècles de science grecque, et en particulier les notions suivantes : sphéricité de la Terre, antipodes, existence d’un continent austral.
L’astronomie mathématise le réel, creusant un écart entre ce qui se donne à l’observation physique et la construction des lois du Cosmos. Jusqu’à Kepler il y a deux astronomies : une astronomie physique et une astronomie mathématique.
Lire le chapitre qu’Alexandre Koyré consacre aux "étapes de la cosmologie scientifique" (pp 87-98 in Etudes d’histoire de la pensée scientifique, tel Gallimard). Comment explique-t-il les résistances à l’idée d’infini ?

